18 May Indicadores de error (error indicator) en Abaqus

¿Sabías que Abaqus/Standard tiene indicadores de error para proporcionar una medida del error local resultante de la discretización de la malla?

En este post entenderas y veras ejemplos de como utilizar el indicador de error (error indicator) de Abaqus/Standard

Introducción a Abaqus/Standard Error indicators

En un análisis de elementos finitos (FEA) basado en el desplazamiento, la tensión suele calcularse a partir del campo de desplazamiento en un paso posterior al procesamiento. Esta tensión calculada, directamente se obtiene a partir de la derivada del campo de desplazamiento, lo que conduce inevitablemente a un campo menos preciso que el del desplazamiento. Por eso, se ha dedicado una cantidad significativa de investigación a recuperar la precisión en el campo de tensiones, lo que ha llevado a métodos conocidos como «técnicas de recuperación de tensiones». Los campos de tensiones mejorados que se obtienen mediante estos procedimientos no sólo proporcionan una mejor representación de las tensiones con un coste computacional reducido, sino que también se utilizan ampliamente en las estimaciones de error a posteriori

Abaqus/Standard determina las variables indicadoras de error basándose en la diferencia entre una distribución suavizada y no suavizada de la solución base, utilizando una técnica de suavizado como la técnica de recuperación de parches de Zienkiewicz y Zhu, (1987). Con esta técnica, la idea es ajustar una aproximación polinómica de orden superior del campo de tensión sobre cada tramo de elementos. La distancia en la norma de energía entre este campo de tensiones suavizado y el campo de tensiones de los elementos finitos se define como una estimación del error.

Una forma de controlar la calidad de una solución de elementos finitos con un uso óptimo de los recursos computacionales es refinar la malla de forma adaptativa. El análisis adaptativo de elementos finitos suele constar de dos etapas: la estimación del error a posteriori y el refinamiento de la malla. El objetivo es refinar la malla de forma que el error esté dentro de la tolerancia especificada y se distribuya lo más uniformemente posible en el dominio.

Enfoque de recuperación de parches superconvergentes

La recuperación de parches superconvergentes (SPR) o Superconverged patch recovery de Zienkiewicz y Zhu, fue ampliamente adoptada y se siguió explorando como una estimación de error a posteriori. En esta técnica de recuperación, la tensión en los nodos de la malla se obtiene utilizando un polinomio completo del mismo orden que el utilizado para aproximar el campo de desplazamiento. El polinomio se ajusta en un sentido de mínimos cuadrados a las tensiones calculadas directamente en puntos superconvergentes, o puntos de muestreo, sobre un fragmento de elementos. De hecho, en estos puntos, la precisión de las derivadas es un orden superior a la de cualquier otro punto del elemento, lo que da lugar a una mejora sustancial de las tensiones correspondientes.

Para los problemas generales no lineales, sólo si se utilizan los puntos de integración como puntos de muestreo, ¿puede aplicarse el método SPR a la recuperación de tensiones?

Tras el análisis de elementos finitos, se define un fragmento para cada vértice dentro del dominio mediante la unión de los elementos que comparten el nodo. En la figura siguiente se muestra un fragmento típico de un elemento cuadrilátero bilineal.

Las variables del error indicator en Abaqus

La discretización por elementos finitos de un dominio del modelo es una aproximación a la solución exacta para todos los análisis. Para ayudarte a entender la extensión y distribución espacial del error de discretización en una solución de elementos finitos, Abaqus/Standard proporciona un conjunto de resultados o outputs que indican el error.

Idealmente, los outputs del indicador de error o (error indicators) deben ser complementadas por otras técnicas, como un estudio de refinamiento de malla, para ganar confianza en que el error de discretización no está degradando significativamente la capacidad del análisis de elementos finitos para hacer predicciones útiles.

De hecho, los indicadores de error pueden ayudar a automatizar un estudio de refinamiento de malla a través de la funcionalidad de reajuste adaptativo de Abaqus/CAE; los resultados de los indicadores de error son utilizadas por esta funcionalidad para determinar dónde refinar o hacer más gruesa una malla.

Resultados de las variables del Error indicator

Estas variables de salida

• Indican el error de discretización en valores de una cantidad y tienen unidades de la solución base (mirar tabla inferior)
• Pueden solicitarse de 3 formas, con las opciones de resultados de elementos o de contactos o como parte de una regla de remallado adaptativo
• Puede normalizarse por formas de la solución base para obtener indicadores de error no dimensionales, como el porcentaje
• En algunos casos, puede aumentar el tiempo de solución del análisis de forma significativa
• Están disponibles en Abaqus/Standard pero no en Abaqus/Explicit

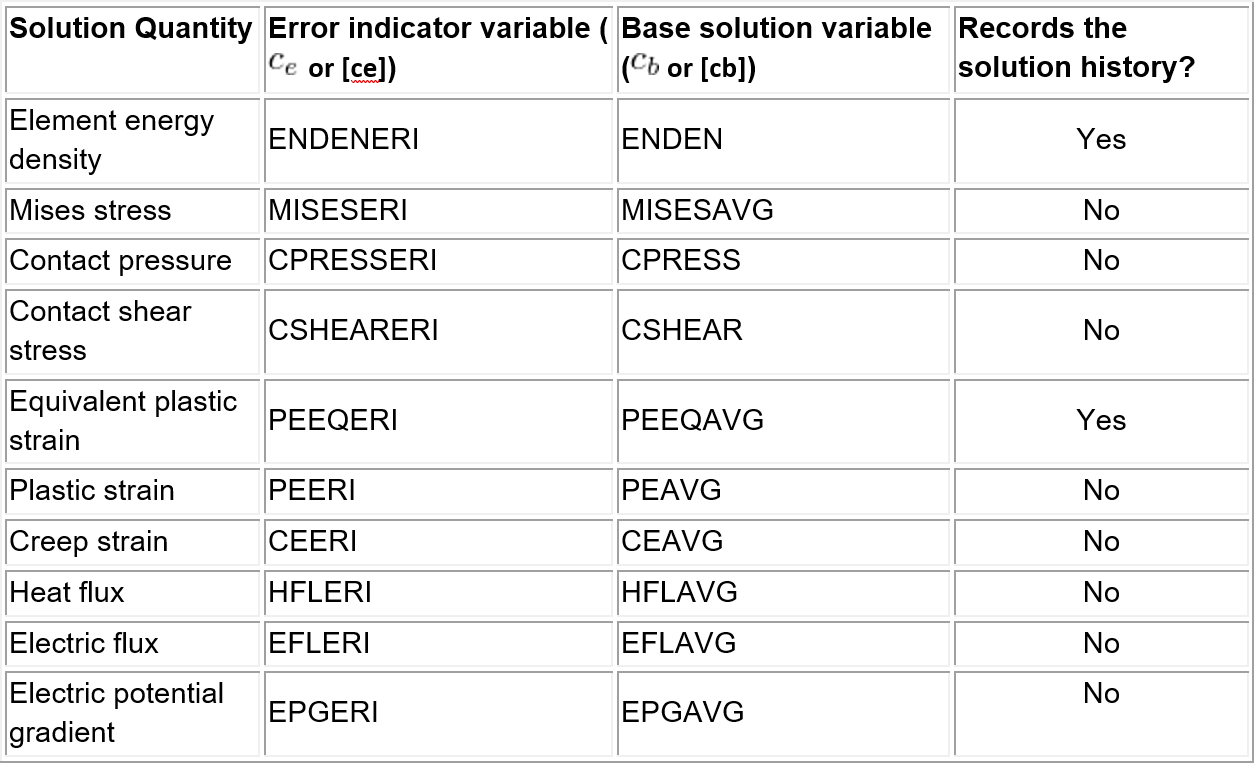
Indicador de error y variables de solución base disponibles en Abaqus/Standard

Las variables indicadoras de error de Abaqus proporcionan una medida del error local resultante de la discretización de la malla. Cada indicador de error (símbolo [ce]) proporciona una indicación de error en una variable base de solución particular (símbolo [cb]). Por ejemplo, el indicador de error de la tensión de Mises, MISESERI, proporciona un indicador de error en la variable de tensión de Mises MISESAVG.

Algunas variables indicadoras de error sólo indican el error de discretización en el tiempo de análisis actual-el incremento particular en un paso. Otras variables indicadoras de error proporcionan un registro de la historia de la solución hasta el tiempo de análisis actual.

La tabla siguiente muestra las diferentes variables que son indicadoras de error disponibles en Abaqus/Standard junto con la correspondiente variable base de la solución e indica si registran la historia de la solución.

Efecto de utilizar outputs del indicador de error en el tiempo de solución

En ocasiones, los cálculos de suavizado aumentan notablemente el tiempo de análisis. Si observa que la adición de una solicitud de salida del indicador de error aumenta significativamente el tiempo de análisis, las estrategias para reducir este efecto incluyen la reducción de la frecuencia de salida y la limitación de la solicitud de salida a una región particular de interés.

para la mayoría de las variables que se analizan, los cálculos del indicador de error sólo ocurren justo antes de escribir la variable del indicador de error en la base de datos de salida, por lo que reducir la frecuencia de salida tenderá a reducir el tiempo de cálculo; sin embargo, este no es el caso del indicador de error de densidad de energía del elemento, porque las contribuciones a este indicador de error se acumulan cada incremento independientemente de si este indicador de error se emite para un incremento dado.

Recomendación: No utilizar ENDENERI a no ser que se requiera la dependencia del historial y el PEEQERI no sea suficiente/aplicable.

Cálculo de medidas normalizadas de error de solución

Se puede utilizar el correspondiente indicador de error y las variables base de la solución [ce] y [cb] respectivamente, para calcular un campo de indicadores de error locales y normalizados

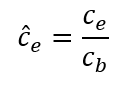
donde [ĉe] es una medida de error normalizada. Por ejemplo,

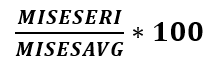
proporciona una forma porcentual del indicador de error basado en la tensión de Mises; sin embargo, esta medida de error normalizada puede no ser particularmente útil, porque

• Tendrá tendencia a llamar la atención sobre las regiones en las que los valores de la solución base son pequeños, que normalmente no son regiones críticas de un diseño
• Tendrá problemas de división por cero cuando el valor de la solución base sea cero

Otros enfoques de normalización, como la normalización basada en una norma global de la variable de la solución base o un valor constante que elijas (como el valor máximo de la solución base permitido en un diseño), pueden ser más eficaces.

Las formas normalizadas de un indicador de error no están disponibles directamente a través de las variables de salida del indicador de error; sin embargo, puede calcular las medidas normalizadas utilizando el módulo de Visualización de Abaqus/CAE (Abaqus/Viewer) para operar sobre los datos de salida del campo. De manera alternativa, se puede utilizar la interfaz de scripting de Abaqus para leer el indicador de error y la solución base de la base de datos de salida y calcular las formas normalizadas.

Interpretación de los resultados del indicador de error

Al interpretar los resultados del indicador de error, se debe recordar que los indicadores de error son medidas aproximadas del error local en la solución base y están, ellos mismos, sujetos a errores de discretización. La precisión de las estimaciones de error tiende a mejorar a medida que se refina la malla. Cada variable del indicador de error tiene las mismas unidades que la correspondiente variable de la solución base, lo que facilita la comparación de las estimaciones locales de la magnitud del error con las estimaciones locales de la solución base.

Regiones de interés de una solución base y el indicador de error correspondiente

La visualización de los resultados de una variable de solución base (CPRESS, por ejemplo) y de la variable indicadora de error correspondiente (CPRESSERI), uno al lado del otro, puede proporcionar una perspectiva útil sobre la precisión de la solución. Por ejemplo, si la solución base se expresa en unidades de tensión, el indicador de error correspondiente también se expresa en unidades de tensión. El siguiente gráfico de contorno muestra los gráficos de contorno de CPRESS y CPRESSERI para un análisis de una esfera presionada en una placa rígida.

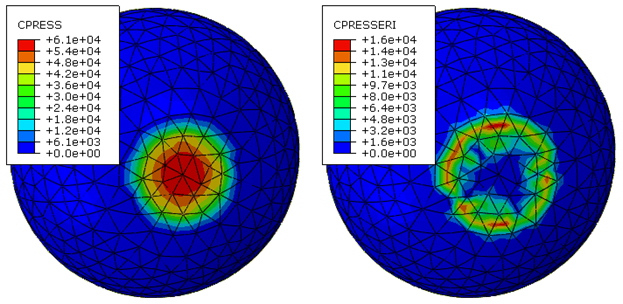
The plot can be interpreted as follows

• La solución de la presión de contacto (CPRESS) es bastante precisa cerca del centro de la región de contacto activa (zona roja de la imagen izquierda), donde la presión de contacto es mayor, porque el indicador de error (CPRESSERI) es una pequeña fracción de la solución base en esa región
• La solución de la presión de contacto (CPRESS) es menos precisa cerca del perímetro de la región de contacto activa(zona verde de la imagen izquierda), donde las variaciones locales en la solución de la presión de contacto son mayores (pero la presión de contacto es significativamente menor que el valor máximo), porque el indicador de error es bastante grande comparado con la solución base en esa región.

El analista debe juzgar que el nivel de refinamiento de la malla es adecuado si la presión máxima de contacto es de interés primordial en tal caso. Si la región de contacto activa fuera significativamente menor que la mostrada en la figura anterior, se necesitaría un refinamiento local de la malla para predecir con precisión la presión máxima de contacto (CPRESS).

Un indicador de error tiende a dar una aproximación cruda y no conservadora de la desviación de la solución exacta si la malla es gruesa en relación con las variaciones locales de la solución o la solución exacta del problema planteado implica una singularidad de tensión.

Las siguientes interpretaciones cualitativas de los resultados del indicador de error que superan aproximadamente el 10% de los resultados de la solución base suelen ser apropiadas:

• «En esta región, existe una posibilidad de inexactitud en la solución bastante significativa».
  «La malla puede ser demasiado gruesa para dar una buena estimación del error de la solución en esta región».
  «Quizás exista una singularidad de tensión en este punto».

Importante: Los resultados del indicador de error son aproximados y no representan una estimación precisa o conservadora de su error de solución. La calidad de un indicador de error puede ser particularmente pobre si su malla es gruesa y mejora a medida que se refina la malla; sin embargo, nunca debe interpretar estas variables como indicación de cuál sería el valor de una variable de solución tras un mayor refinamiento de la malla.

Caso de Ejemplo: Indicadores de error para diferentes densidades de malla

Indicador de error Abaqus de una varilla: introducción

El siguiente caso de ejemplo se refiere a una varilla con sección transversal rectangular sometida a una carga gravitatoria. Este caso se analizó seis veces utilizando diferentes densidades de malla; en cada ejecución posterior se duplicó la cantidad de elementos en dirección axial. Los elementos que se utilizaron son de tipo C3D8R lineal de 8 nodos, integración reducida, control de reloj de arenaLa figura siguiente muestra la varilla con la malla inicial compuesta por tres elementos. La carga gravitacional se aplica en el eje Z positivo.

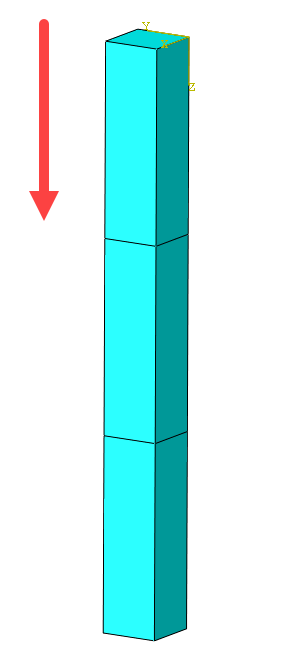
Resultados de tension en la varilla

La figura siguiente muestra los resultados de tensiones [MPa] para cada modelo con diferente densidad de malla, empezando por un modelo con 3 elementos, hasta 6, 12, 24, 48 y 96.

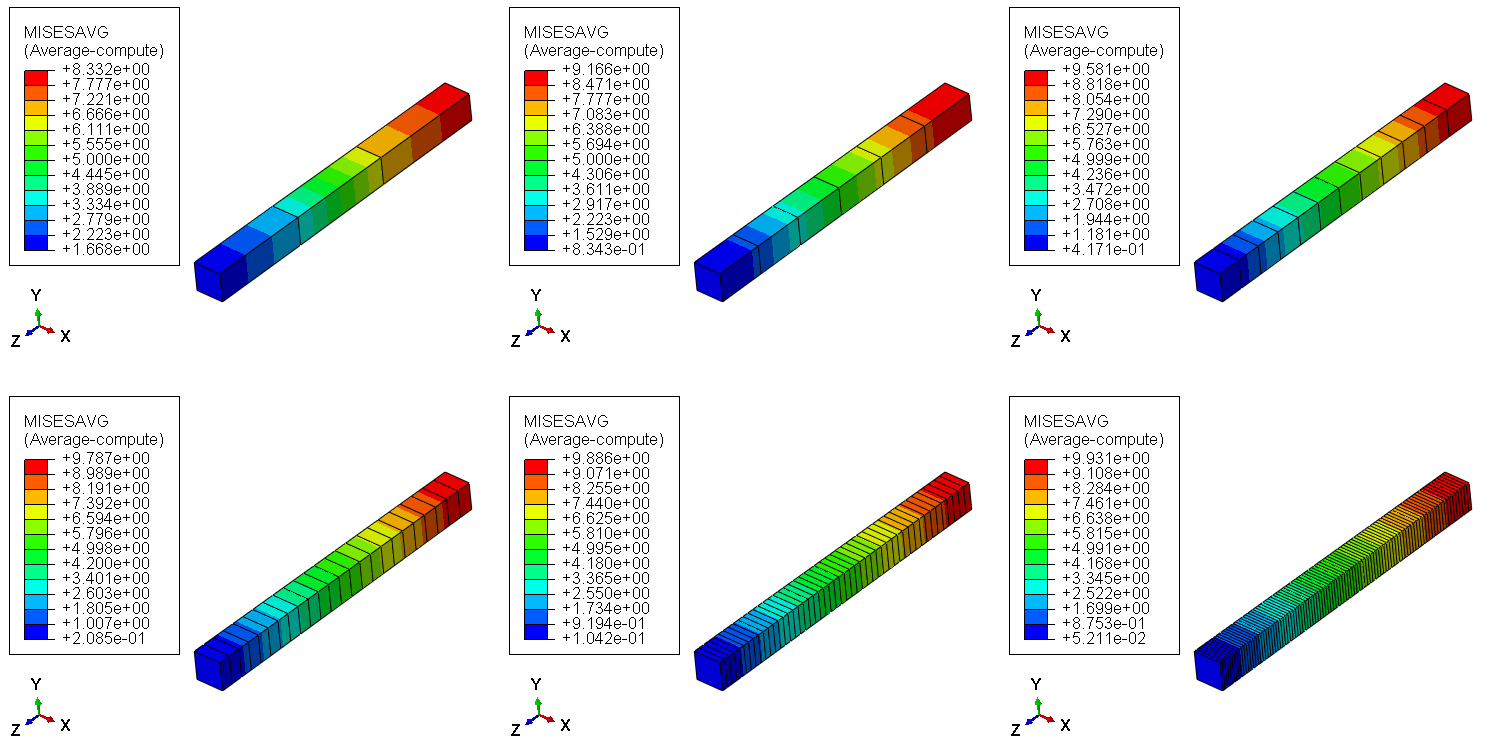
En este sencillo caso se observa fácilmente el error de discretización creado por las diferentes densidades de malla. Como referencia, el cálculo de la tensión a mano sería de 10 [MPa] en el extremo fijo de la varilla y de 0 [MPa] en el extremo libre de la misma.

Cabe mencionar que el valor más bajo de la tensión en cada modelo se reduce aproximadamente a la mitad para cada densidad de malla posterior, debido a la posición del punto de integración sobre la longitud de la varilla. A medida que la dimensión del elemento en la dirección axial de la varilla se hace más pequeña, los puntos de integración del primer y último elemento se acercan a los límites físicos de la varilla y el valor de la tensión calculada en esos puntos de integración se acerca al cálculo analítico de 0 [MPa] y 10 [MPa].

Resultados del indicador de error de la varilla

Para este caso tan sencillo, podría ser posible estimar la salida del indicador de error utilizando un enfoque muy simple. La figura siguiente es un gráfico que muestra la distribución de tensiones en la longitud de la varilla.

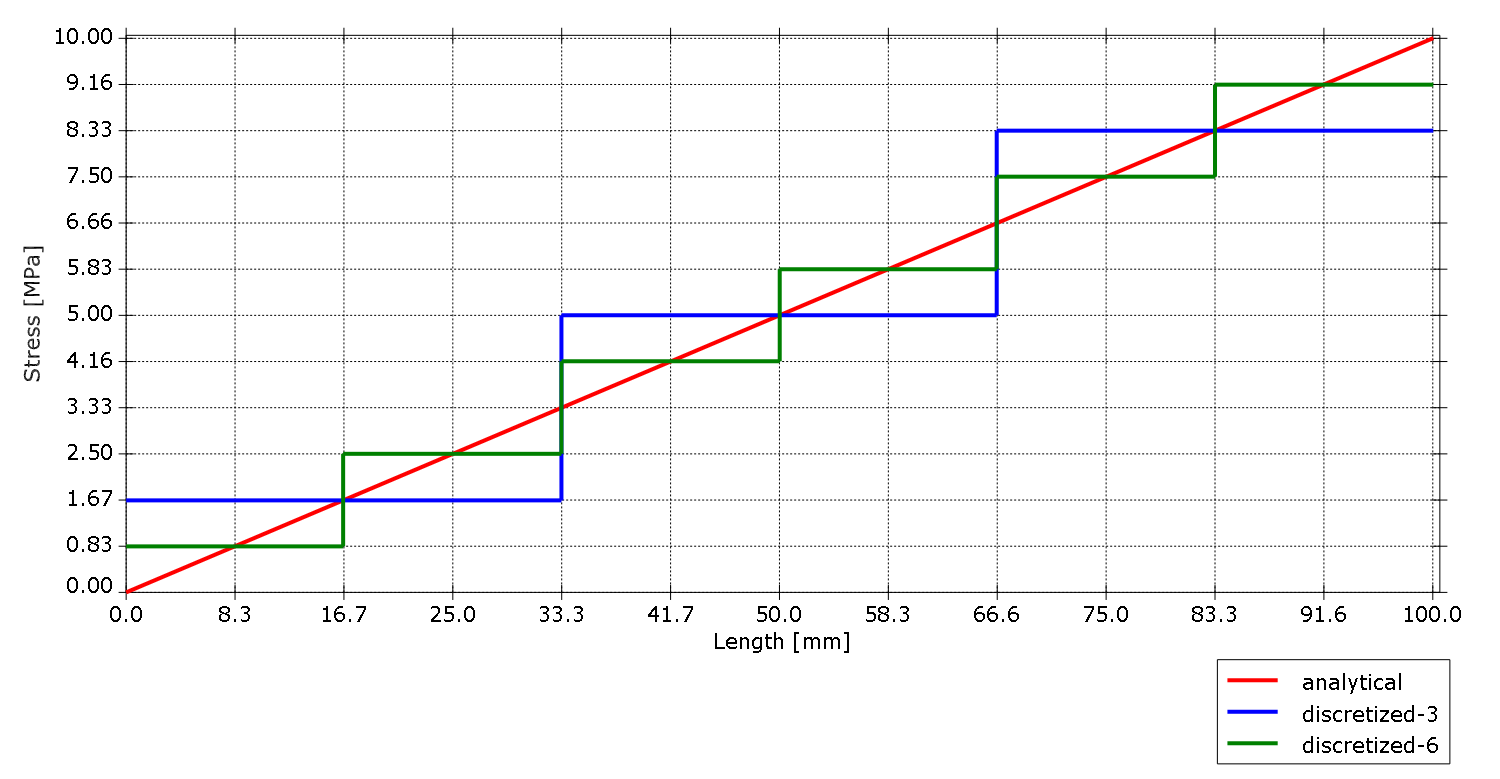
Los tres gráficos diferentes  se refieren al cálculo analítico de la tensión (rojo) junto con el cálculo discretizado utilizando una malla de tres elementos (azul)  y una malla de seis elementos (verde).

A partir de este gráfico superior se puede calcular fácilmente que, para el primer elemento del modelo de tres elementos (desde 0 a 33.3 [mm]), el error en los nodos del elemento es de ~1.67 [MPa] y el error desciende linealmente hasta 0 [MPa] en el punto de integración en el centro del elemento (16.7 [mm]), punto en el que da el mismo valor el resultado analítico (rojo) y el discretizado (azul).

El valor de error promediado en todo el elemento puede ser calculado como la mitad de los máximos, que sería 1.67/2 = ~0.83 [MPa], que es una estimación sencilla del error de discretización y una predicción para, al menos, tener una idea del orden de magnitud de los resultados del indicador de error que Abaqus calculará.

Siguiendo el mismo enfoque simple para el modelo de seis elementos, se puede observar fácilmente que el error estimado será aproximadamente la mitad del valor del modelo de tres elementos, lo que lleva a la conclusión de que la duplicación de la cantidad de elementos a lo largo de la longitud de la varilla conduce a la mitad del valor del indicador de error.

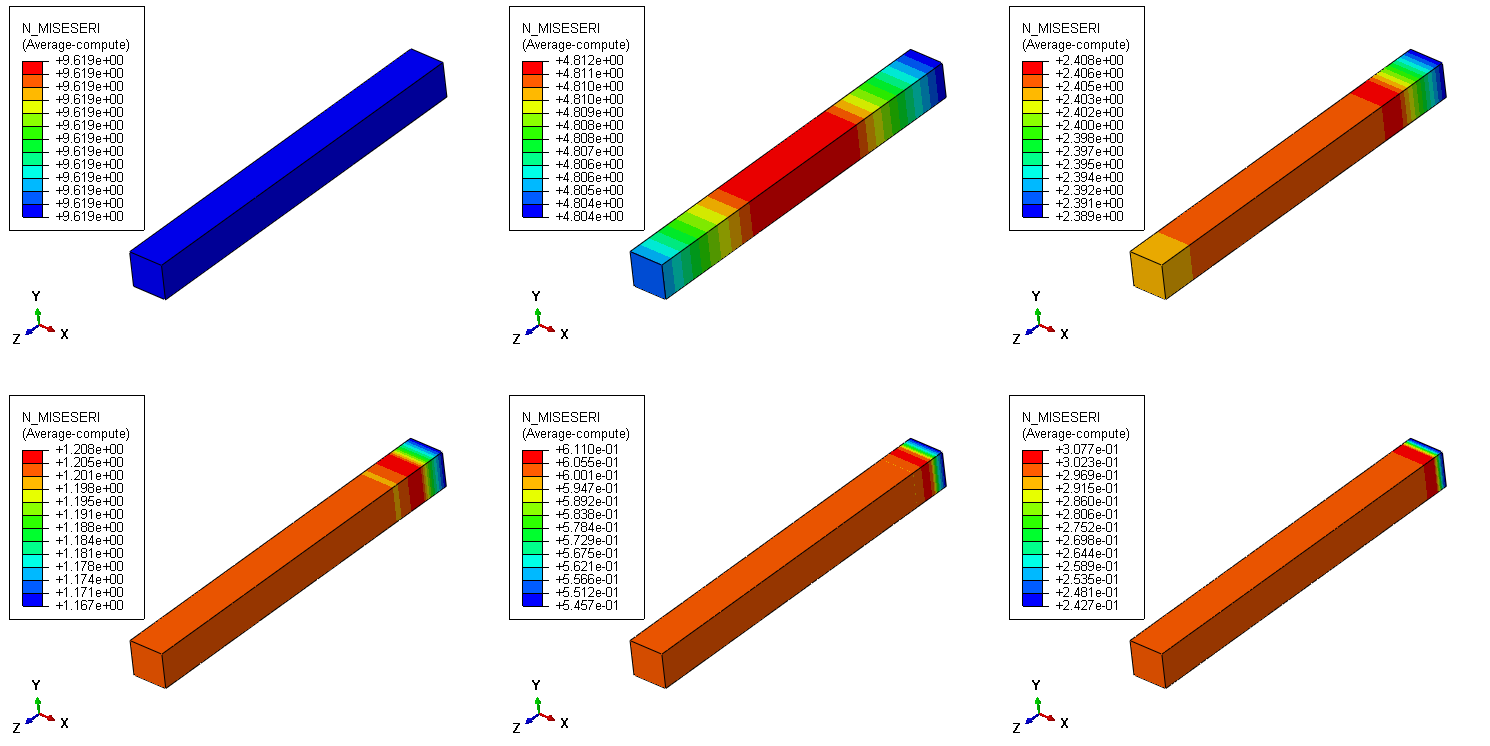
La figura siguiente muestra la correspondiente salida del indicador de error (MISESERI) para los seis modelos con las diferentes densidades de malla.

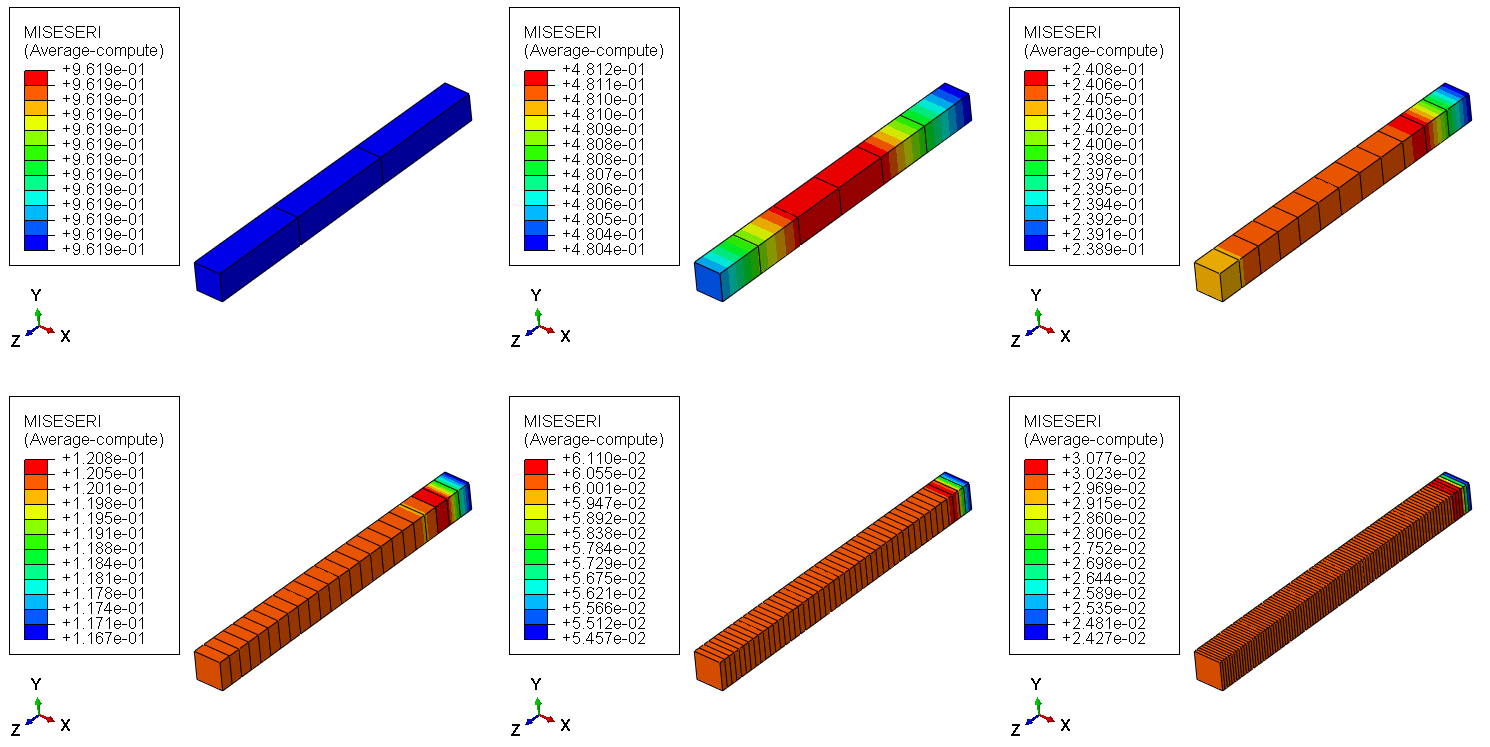
El error estimado de ~0.83 [MPa] para el modelo de tres elementos no se cumple exactamente ya que nos da 0.961 [Mpa], pero el valor estimado se aproxima bastante al calculado y se trata de una aproximación a cómo se calcula este resultado.

Además, la suposición de que el valor de salida del indicador de error se reducirá a la mitad por cada duplicación de los elementos, se cumple realmente, por lo que se nota la influencia de la densidad de la malla en el valor del indicador de error. Este valor debe ser comparado con el valor de la solución base para estimar el tamaño del error introducido por la discretización de la malla y si se desea un mayor refinamiento de la misma.

Resultados del indicador de error normalizado de la varilla

La figura siguiente muestra el resultado normalizado del MISESERI que se calcula a partir de la fórmula

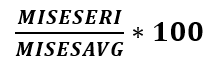
Muestra el porcentaje del valor del indicador de error sobre el valor de los resultados de tensión calculada por el análisis mediante elementos finitos (FEA).

El valor máximo del resultado normalizado de MISESERI es similar entre todos los modelos (~57.6 [MPA]). Esto se debe al hecho de que, basándose en la fórmula utilizada anteriormente, a la vez que el valor de los resultados del indicador de error se reducía a la mitad cuando se duplicaba la cantidad de elementos, tambien ser reducía a la mitad el valor de tensión más bajo ya que seguía exactamente la misma tendencia con respecto a la densidad de la malla. Por lo tanto, el máximo error normalizado aparece en el extremo libre de la barra donde el valor de la solución base es el más bajo, lo que puede ser confuso y engañoso.

Por esta razón, se calculó un resultado normalizado diferente basado en la fórmula

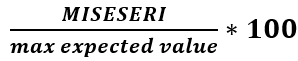
En este caso, el valor máximo esperado es, como ya se ha mencionado, 10 [MPa].

Los resultados de esta salida normalizada actualizada se muestran en la imagen siguiente.

El resultado del indicador de error normalizado actualizado es más descriptivo, en este caso concreto, en cuanto a la cantidad de error en cada modelo. Este resultado oscila entre el 9,6% para el modelo de tres elementos y el 0,3% para el modelo de noventa y seis elementos.

Este umbral entre mallado grueso o fino debe ser fijado por el analista para identificar la densidad de malla ideal y el equilibrio entre el coste computacional y el error de discretización aceptado.

BONUS: Resultados de la simulación VCollab

El siguiente archivo muestra un informe interactivo en 3D de los resultados de la simulación descritos anteriormente.

No dudes en iteractuar con los resultados, rotando, zoom in, zoom out o pasar entre las diferentes paginas.

Consideraciones adicionales para la evaluacion de los indicadoras de error de los elementos

Cuando se solicita la salida del indicador de error del elemento, la solicitud sólo debe aplicarse a los elementos admitidos para la salida del indicador de error.

La técnica de recuperación de fragmentos utilizada para calcular las variables del indicador de error de elementos asume que la solución debe ser continua sobre el conjunto de elementos especificado.

Limitations

Sólo se admiten los siguientes tipos de elementos para los cálculos de los indicadores de error

• Elementos planos continuos triangulaes y cuadriláteros
• Elementos shell triangulares y cuadriláteros
• Tetraédricos
• Hexaédricos

No se admiten elementos con nodos variables.
No se admite la salida del indicador de error en los siguientes casos

• Import analysis
• Restart analysis
• Post output analysis
• Map solution analysis
• Symmetric model generation analysis

Referencias

[1] Zienkiewicz, O. C., & Zhu, J. Z. (1987). A simple error estimator and adaptive procedure for practical engineering analysis. International journal for numerical methods in engineering, 24(2), 337-357.
[2] González-Estrada, O. A., Nadal, E., Ródenas, J. J., Kerfriden, P., Bordas, S. P. A., & Fuenmayor, F. J. (2014). Mesh adaptivity driven by goal-oriented locally equilibrated superconvergent patch recovery. Computational Mechanics, 53(5), 957-976.
[3] Oh, H. S., & Batra, R. C. (1999). Application of Zienkiewicz–Zhu’s error estimate with superconvergent patch recovery to hierarchical p-refinement. Finite elements in analysis and design, 31(4), 273-280.
[4] Gu, H., Zong, Z., & Hung, K. C. (2004). A modified superconvergent patch recovery method and its application to large deformation problems. Finite Elements in Analysis and Design, 40(5-6), 665-687.
[5] Sharma, R., Zhang, J., Langelaar, M., van Keulen, F., & Aragón, A. M. (2018). An improved stress recovery technique for low‐order 3D finite elements. International Journal for Numerical Methods in Engineering, 114(1), 88-103.

¿Necesitas mas información?

No dude en ponerse en contacto con contacto@4realsim.com si necesita ayuda.