28 May Abaqus Anisotropic Hyperelasticity

The anisotropic hyperelastic model provides a general capability for modeling materials that exhibit highly anisotropic and nonlinear elastic behavior (such as biomedical soft tissues and fiber-reinforced elastomers). The model is valid for large elastic strains and captures the changes in the preferred material directions (or fiber directions) with deformation.
The anisotropic hyperelastic material model can be used in combination with large-strain time-domain viscoelasticity; however, the viscoelasticity is isotropic. Furthermore it optionally allows the specification of energy dissipation and stress softening effects.
This blog post is based on the Anisotropic Hyperelastic Behavior of the Abaqus manual.

Anisotropic Hyperelasticity Formulations

Many materials of industrial and technological interest exhibit anisotropic elastic behavior due to the presence of preferred directions in their microstructure. Examples of such materials include common engineering materials (such as fiber-reinforced composites, reinforced rubber, and wood) as well as soft biological tissues (arterial walls, heart tissue, etc.). When these materials are subjected to small deformations (less than 2–5%), their mechanical behavior can generally be modeled adequately using conventional anisotropic linear elasticity. Under large deformations, however, these materials exhibit highly anisotropic and nonlinear elastic behavior due to rearrangements in the microstructure, such as reorientation of the fiber directions with deformation. The simulation of these nonlinear large-strain effects calls for more advanced constitutive models formulated within the framework of anisotropic hyperelasticity. Hyperelastic materials are described in terms of a “strain energy potential, which defines the strain energy stored in the material per unit of reference volume (volume in the initial configuration) as a function of the deformation at that point in the material. Two distinct formulations are used for the representation of the strain energy potential of anisotropic hyperelastic materials: strain-based and invariant-based.

Strain-Based Formulation

In this case the strain energy function is expressed directly in terms of the components of a suitable strain tensor, such as the Green strain tensor. The underlying assumption in models based on the strain-based formulation is that the preferred material directions are initially aligned with an orthogonal coordinate system in the reference (stress-free) configuration. These directions might become nonorthogonal only after deformation. Examples of this form of strain energy function include the generalized Fung-type form described below.

Invariant-Based Formulation

Using the continuum theory of fiber-reinforced composites the strain energy function can be expressed directly in terms of the invariants of the deformation tensor and fiber directions.
Unlike for the case of the strain-based formulation, in the invariant-based formulation the fiber directions need not be orthogonal in the initial configuration. An example of an invariant-based energy function is the form proposed by Holzapfel, Gasser, and Ogden for arterial walls.

Anisotropic Strain Energy Potentials

Abaqus strain energy potential available forms

There are four forms of strain energy potentials available in Abaqus to model approximately incompressible anisotropic materials:

• the generalized Fung form (including fully anisotropic and orthotropic cases),
• the Holzapfel-Gasser-Ogden form for arterial walls,
• the Holzapfel-Ogden form for passive myocardium tissue, and
• the Kaliske-Schmidt form for reinforced polymeric materials and biomaterials. You can find an example here.

These forms are adequate for modeling soft biological tissue. However, whereas Fung’s form is purely phenomenological, the other forms are micromechanically based.

Strain energy potential user subroutines

In addition, Abaqus provides a general capability to support user-defined forms of the strain energy potential via two sets of user subroutines: one for strain-based and one for invariant-based formulations. For both methods, either compressible or incompressible behavior can be specified in Abaqus/Standard; only nearly incompressible behavior is allowed in Abaqus/Explicit.
User-Defined Form: Strain-based
You can define the form of a strain-based strain energy potential directly with user subroutine UANISOHYPER_STRAIN in Abaqus/Standard or VUANISOHYPER_STRAIN in Abaqus/Explicit. The derivatives of the strain energy potential with respect to the components of the modified Green strain and the elastic volume ratio must be provided directly through these user subroutines.
User-Defined Form: Invariant-Based
You can define the form of an invariant-based strain energy potential directly with user subroutine UANISOHYPER_INV in Abaqus/Standard or VUANISOHYPER_INV in Abaqus/Explicit.

Compressibility

Most soft tissues and fiber-reinforced elastomers have very little compressibility compared to their shear flexibility. This behavior does not warrant special attention for plane stress, shell, or membrane elements, but the numerical solution can be quite sensitive to the degree of compressibility for three-dimensional solid, plane strain, and axisymmetric elements. In cases where the material is highly confined (such as an O-ring used as a seal), the compressibility must be modeled correctly to obtain accurate results. In applications where the material is not highly confined, the degree of compressibility is typically not crucial; for example, it would be quite satisfactory in Abaqus/Standard to assume that the material is fully incompressible: the volume of the material cannot change except for thermal expansion.

Thermal Expansion

Both isotropic and orthotropic thermal expansion is permitted with the anisotropic hyperelastic material model.

Viscoelasticity

Anisotropic hyperelastic models can be used in combination with isotropic viscoelasticity to model rate-dependent material behavior. Because of the isotropy of viscoelasticity, the relaxation function is independent of the loading direction. This assumption might not be acceptable for modeling materials that exhibit strong anisotropy in their rate-dependent behavior; therefore, this option should be used with caution.
The anisotropic hyperelastic response of rate-dependent materials can be specified by defining either the instantaneous response or the long-term response of such materials.

Stress Softening

The response of typical anisotropic hyperelastic materials, such as reinforced rubbers and biological tissues, under cyclic loading and unloading usually displays stress softening effects during the first few cycles. After a few cycles the response of the material tends to stabilize and the material is said to be preconditioned. Stress softening effects, often referred to in the elastomers literature as Mullins effect, can be accounted for by using the anisotropic hyperelastic model in combination with the pseudo-elasticity model for Mullins effect in Abaqus. The stress softening effects provided by this model are isotropic.

Example: Anisotropic hyperelastic modeling of arterial layers

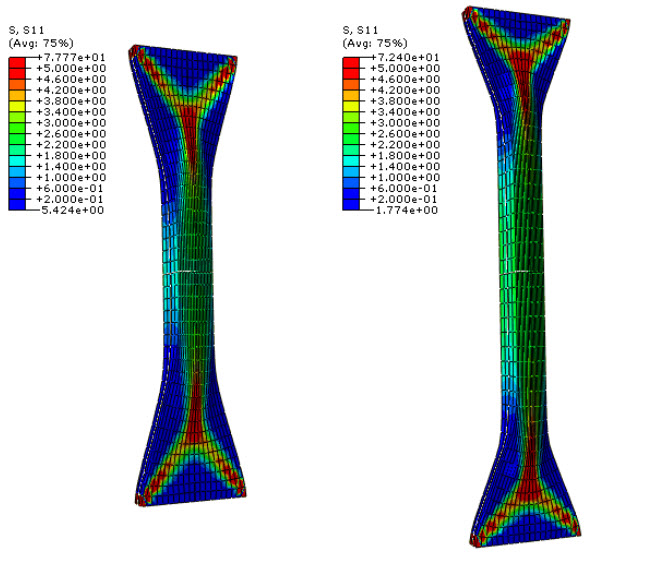
This problem illustrates the use of the anisotropic hyperelastic capabilities in Abaqus to model soft biological tissue. More specifically, the problem shows how these capabilities can be used to model the mechanical response of the adventitial layer of human iliac arteries.
Numerical examples are provided for simple tension tests of iliac adventitial strips cut along the axial and circumferential directions of the artery. An example of a strip cut at an angle of 15° with respect to the circumferential direction is also included. The numerical study demonstrates the significant effect that dispersion of the collagen fiber orientations can have on the mechanical response of soft tissue. The problem has been analyzed numerically by Gasser, Holzapfel, and Ogden.

Anisotropic hyperelastic consultancy

4RealSim has a proven track record in providing engineering services to model anisotropic hyperelasticity. Contact us at sales@4realsim.com if you want to discuss your case or are interested to acquire the right software to perform these simulations.