14 May Abaqus for dummies: Understanding the Complexities of Gasket Analysis

Getting started with Abaqus Introduction

Hello everyone, I’m Tijmen and thank you for following my journey to Start with Abaqus, Download and install the Abaqus learning edition and Get started with Abaqus.
Let’s continue the blog series dedicated to exploring the vast capabilities of Abaqus. Over the coming months, we will embark on a journey through various example problems, unraveling the multitude of options and possibilities that Abaqus has to offer.
For engineers, researchers, and enthusiasts alike, Abaqus stands as a beacon of innovation, empowering users to simulate and analyze complex mechanical behaviors with unparalleled accuracy. However, navigating through its extensive features and functionalities can sometimes feel daunting.
In this series, we aim to demystify Abaqus by breaking down example problems into digestible segments, allowing you to grasp its essence and harness its full potential. Whether you’re a novice seeking to enhance your skills or a seasoned professional looking to delve deeper, this series will cater to your needs.
Each blog post will delve into a specific example problem, we will look at some animations and discuss the analysis. Through this series, our goal is not only to showcase the capabilities of Abaqus but also to inspire creativity and foster a deeper understanding of finite element analysis concepts. We encourage active participation, questions, and feedback from our readers, as together, we embark on this educational journey.

Understanding the Complexities of Gasket Analysis

In the realm of engineering, components undergoing significant deformation often exhibit folding, with different surface areas coming into contact. Predicting these contact points upfront can pose challenges, complicating the definition of independent surfaces for analysis.
Consider the application of this principle in analyzing an oil pan gasket, crucial for sealing the interface between the oil pan and the engine block. Designers aim to achieve a specific threshold of contact pressure at critical interfaces to prevent oil leakage. Moreover, understanding the load-deflection curve aids in determining the bolt load required to maintain the desired gap between components.
In this analysis, the rubber gasket, housed within a plastic backbone, plays a pivotal role. With two planes of symmetry and a sealing bead, its compression ensures effective sealing. The gasket’s geometry leads to folding in two distinct locations, necessitating a comprehensive modeling approach.
In this model, the entire free surface of both the gasket and backbone is treated as a single surface allowed to contact itself. While this simplifies the analysis, it increases computational complexity, particularly with extensive contact searches, and a larger equation system, notably in Abaqus/Standard.
To explore these intricacies, the analysis employs both Abaqus/Standard and Abaqus/Explicit, offering a comprehensive understanding of the gasket’s behavior under different conditions.

Geometry and model of the rubber gasket

The rubber gasket is represented as a quarter of a plane strain section initially in contact with a flat rigid surface. There is a 0.612 mm clearance between the plastic backbone and the surface, with a bead height in the gasket of 1.097 mm. The backbone is characterized by a linear elastic material with a Young’s modulus of 8000.0 MPa and a Poisson’s ratio of 0.4.

In Abaqus/Standard, the gasket is modeled as a fully incompressible hyperelastic material, softer than the backbone material at all strain levels. Conversely, in Abaqus/Explicit, a small amount of compressibility is assumed for the gasket material. The gasket’s nonlinear elastic behavior is described by a first-order polynomial strain energy function.
The model utilizes first-order quadrilaterals for discretization, employing standard elements for the backbone. In Abaqus/Standard, full-integration hybrid elements are used for the gasket, while reduced-integration elements are employed in Abaqus/Explicit.
The interface between the gasket and the backbone is assumed to be glued, requiring no special treatment. A single surface definition encompasses the free surfaces of both the gasket and the backbone. This surface is allowed to contact both the rigid surface and itself through the definition of contact pairs. A slight amount of friction (Coulomb coefficient of 0.05) is applied to the interface with the rigid surface, presumed to be lubricated. Sticking surface behavior, specified through rough friction (Frictional Behavior), is enacted when the gasket contacts itself, indicating a clean surface.

Abaqus rubber gasket Results and discussion

Below you can find a 3D interactive html report. The best way to review the results in this report is clicking on the 3 dots and select the Full screen option from the list (the last option from the list).

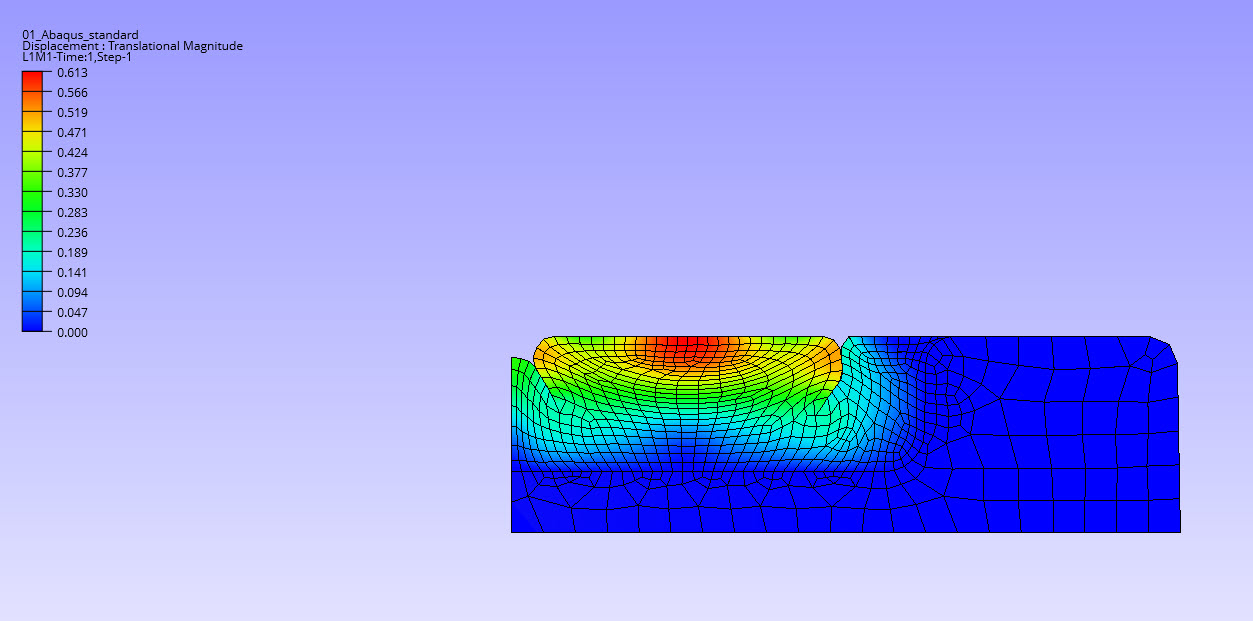
The gasket analysis unfolds as a single-step process, with the rigid surface gradually descending to minimize the backbone clearance (0.61 mm). As the backbone maintains its relative rigidity, the rubber gasket is compelled to conform within its confines, resulting in distinct folding at two regions (see viewpoint 5 and 6 in the VCollab report above). Although initial estimations hint at the general vicinity of fold locations, pinpointing their exact positions proves elusive.
Across both Abaqus/Standard and Abaqus/Explicit analyses, there’s remarkable agreement in predicting the gasket’s deformed shape and fold locations. Additionally, the load-displacement curve of the rigid surface exhibits consistent alignment between the two analyses, as illustrated in viewpoint 4 in the VCollab report.

Rubber foam Abaqus reference

This blog post is based on the “Self-contact in rubber/foam components: rubber gasket” from the Abaqus Example Problem manual. More details can be found here.

Do you have questions about this blog post or do you want to be informed when the next post is released? Contact me at tijmen@4realsim.com.